I was recently asked “Why does the Lasso induce sparsity?” My reflex was to proceed to describe the image we have all seen in our stats/ML classes:

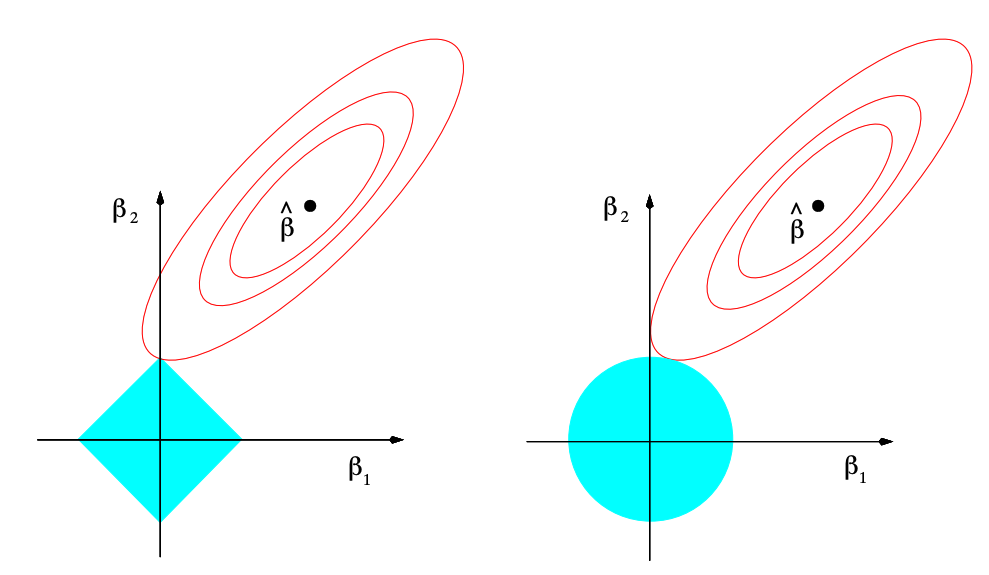
I said something like: “On the left, the level set of the function we are trying to minimize hits the $l_1$ ball right in one of the corners, which induces sparsity; the same thing happens in higher dimensions. When you use the $l_2$ norm, there is no reason you should expect sparsity, as shown in the right side of the image.” This person replied with “well that’s actually not a good explanation…” Not gonna lie, I was surprised by their answer.

I’ve had many interactions with people regarding sparsity and the Lasso, and every single time my explanation had sufficed (to the point where I believed it was a good explanation). Seeing I was stumped, this person asked me if I was familiar with the “soft-thresholding” operator. This sounded familiar but I couldn’t really use the hint to improve my explanation.

If my memory doesn’t fail me, I think I got out of trouble by saying something like: “Well, we should probably look at the optimality conditions and analyze them. With this we should be able to explain why sparsity arises,” and thankfully we moved on to talk about something else.

Later I came back to think about this question and tried to come up with a good explanation. After spending a couple hours, I was unsuccessful (if you are curious, my failed attempt is in the Appendix). However, something good that came out of doing all this thinking is that I realized I had fooled myself into thinking I understood something just because someone showed me a pretty picture and told me that was the right explanation. This reminded me of Feynman’s quote: “The first principle is that you must not fool yourself and you are the easiest person to fool.”

The Lasso

Let me stop for a second and revisit the Lasso. Suppose you have $n$ samples $(x_i, y_i) \in \mathbb{R}^p \times \mathbb{R}$. You want to solve the following optimization problem:

\begin{align} \min_{\beta} \sum_{i=1}^n (y_i - x_i^\top \beta)^2 \cr \Vert \beta \Vert_1 \leq k \tag{1} \end{align}

for some $k \in \mathbb{R}_+$. Equivalently (by relaxing the constraint) we have

\begin{align} \min_{\beta} \sum_{i=1}^n (y_i - x_i^\top \beta)^2 + \lambda \Vert \beta \Vert_1 \tag{2} \end{align}

for some $\lambda \in \mathbb{R}_+$. So the question we want to answer is: If $\beta^* \in \mathbb{R}^p$ is the optimal solution to the Lasso problem, why will $\beta^{\star}$ have many entries exactly equal to zero?

Why Is The Picture a Bad Explanation?

So, why is Figure 1 a bad explanation? At first glance it does seem to show how, in this specific example, that the level-set of the function we are trying to minimize touches the $l_1$ ball in one of the corners. However, there are plenty of other problems (with corresponding level-sets) that will intersect the $l_1$ ball in the middle of a line segment (to see this, just think about dragging around the function around so that its level set touches the edge of the $l_1$ ball).

Additionally, the image is trying to make an argument that relies on the shape of the $l_1$ ball to explain sparsity. But we know that shrinking $k$ in Eq. 1 (or increasing $\lambda$ in Eq. 2) leads to sparser solutions. An argument for sparsity that relies solely on the shape of the ball fails to explain why shrinking $k$ (increasing $\lambda$) induces more sparsity. You could argue that the smaller $k$ is, the smaller the faces of the $l_1$ ball are, so the higher the chance the level set hits the ball in a kink. However, this is still very hand-wavy, and I don’t think is a good explanation.

A Slightly Better Explanation

As I mentioned earlier, I tried to come up with an explanation for the sparsity of the Lasso by myself. But I didn’t make good progress in a reasonable amount of time so I went online in search for a good explanation. I came across these notes by Ryan Tibshirani and found a mention of the “soft-thresholding operator”. It turns out that under certain conditions, which I’ll explain shortly, this “soft-thresholding operator” is indeed a good explanation for sparsity. Let’s explore why. The optimality condition on (2), i.e. setting the (sub)gradient equal to 0, tells us that for every $i=1,…, d$ we have that:

$-x_{1, i} (y_1 - x_1^\top \beta^*) - x_{2, i} (y_2 - x_2^\top \beta^*) - ... - x_{n, i} (y_n - x_n^\top \beta^*) + \lambda v_i = 0 \tag{3}$

where $v_i$ is an element in the subdifferential of $\vert \cdot \vert$ at $\beta_i^*$. That is, $v_i$ is the set:

$v_i = \begin{cases} \{-1\} & \text{if } \beta_i^* < 0 \\ \{1\} & \text{if } \beta_i^* > 0 \\ [-1, 1] & \text{if } \beta_i^* = 0. \end{cases}$

Now, let’s rewrite Equation 3 using matrix notation, we have that for all $i=1,…, d$

$-X_i^\top (y - X \beta^*) + \lambda v_i = 0.$

Rearranging terms we get

$X_i^\top y - \lambda v_i = X_i^\top X \beta^*.$

Here is where those “certain conditions” I mentioned earlier are needed for us to arrive to the “soft-thresholding operator”. When the columns of $X$ are orthogonal to each other (we will explore what this intuitively means is a sec), that is $X_j^\top X_k = 0$ for $j\neq k$, and $X_j^\top X_j = 1$, we have that:

$X_i^\top y - \lambda v_i = \beta^*_i \tag{4}.$

And now, we have three cases.

Case 1. If $\beta^*_i > 0$, then $v_i = 1$, by Eq. 4 it must be that $\beta_i= X_i^\top y -\lambda $, which of course only happens when $X_i^\top y > \lambda$.

Case 2. If $\beta^*_i < 0$, then $v_i = -1$, by Eq. 4 it must be that $\beta_i= X_i^\top y +\lambda $, which of course only happens when $X_i^\top y < -\lambda$.

Case 3. If $\beta^*_i = 0$ then $v_i \in [-1, 1]$, by Eq. 4 this can only happen when $\frac{X_i^\top y}{\lambda} = v_i$ for some $v_i \in [-1, 1]$. Which can only be true if and only if $\vert X_i^\top y \vert \leq \lambda$.

We have shown that when the columns of $X$ are orthogonal to each other and $X_i^\top X_i = 1$ for $i=1,…,p$, then

$\beta^*_i = \begin{cases} X_i^\top y -\lambda & \text{if } X_i^\top y > \lambda\\ X_i^\top y +\lambda & \text{if } X_i^\top y < -\lambda \\ 0 & \text{if } \vert X_i^\top y \vert \leq \lambda. \end{cases}$

Notice that when $\vert X_i^\top y \vert \leq \lambda$, $\beta_i$ is thresholded to 0, when $X_i^\top y > \lambda$ and the term $X_i^\top y$ increases then so does $\beta_i$, finally, when $X_i^\top y < \lambda$ and $X_i^\top y$ decreases, so does $\beta_i$. This is where the “soft-tresholding” name comes from.

I’d say that we now have a better explanation of why the Lasso induces sparsity, however, the explanation is not complete. It only works when the columns of $X$ are orthogonal to each other and $X_i^\top X_i = 1$ for $i=1,…,p$. The second part, $X_i^\top X_i = 1$, is not a big deal since we would still get soft thresholding but with a different constant. However, in the context of regression, what does it mean for the columns of $X$ to be orthogonal? Is this a strong assumption? I think the answer is yes. When every feature has been mean-cenetered, when $j\neq k$ then $X_j^\top X_k = 0$ is equivalent to $\sum_{i=1}^n x_{i,j} x_{i,k} = 0$ which just means that features $j$ and $k$ are uncorrelated. This is a strong assumption, so I think that at this point, our “soft thresholding operator” explanation for sparisty is still limited. What happens if some of our features are not uncorrelated, will the Lasso still force sparsity?

The Correct Explanation

In these slides from François Fleuret I found the cleanest explanation for why Lasso induces sparsity. It turns out sparsity is a property of regularizing using the $l_1$-norm rather than something specific to the Lasso problem, i.e. the $\sum_{i=1}^n (y_i - x_i^\top \beta)^2$ term does not matter too much (except that it is convex in $\beta$). He states the following:

Lemma. Let $\mathcal{L}(w)$ be a convex function and let $w^* \in \arg \min_{w \in \mathbb{R}^p} \mathcal{L}(w) + \lambda \Vert w \Vert_1$. Assume that $\mathcal{L}(w)$ is differentiable at $w^\star$ (I think this can be relaxed, but makes the argument messier). Then, if $-\lambda < \frac{d\mathcal{L}(w^*)}{dw_i} < \lambda$ for any $i=1,…, p$, we have that $w^{\star}_i = 0$.

Proof. By optimality conditions (setting the subgradient to 0) we have that for every $i=1,…, p$

$\frac{\partial L(w^*)}{\partial w_i} + \lambda v_i = 0,$

where you should recall that $v_i$ is an element in the subdifferential of $\vert \cdot \vert$ at $w_i^*$. Rearranging terms we get that for every $i=1,…, p$

$v_i = \frac{-\frac{\partial L(w^*)}{\partial w_i}}{\lambda},$

so that when $-\lambda < \frac{d\mathcal{L}(w^*)}{dw_i} < \lambda$ it must be the case that $v_i \in (-1,1)$ which implies that $w_i=0$. $\square$

Beautiful :)

Final Thoughts

I find it interesting that what I’m calling “the correct explanation” is, in my opinion, the shortest and easiest argument to follow. This could be because the statement of the Lemma was given to us (and coming up with the statement was actually the hard part), and once you know what must be proved the proof is easy.

Something else I find interesting is that the correct explanation does not make the soft thresholding operator pop up. So, I wonder if the person who posed the question understands the reason for sparsity in the same way that we do now.

My last thought is that I should think about Feynman’s quote more often: “The first principle is that you must not fool yourself and you are the easiest person to fool.”

Appendix

My Failed Attempt

I only briefly describe my attempt since I don’t think it’s that insightful. The main reason I write it down is so that you, the reader, who is probably incredibly curious and tried explaining the sparsity of the Lasso yourself (or let’s face it, you have a crush on me and that’s why you are reading even the Appendix of this blog post), does not feel discouraged. Math is hard for most of us, but so what, it’s a beautiful endeavor and we are struggling together. Ok, enough nonsense, let me describe my failed attempt.

I started by looking at the formulation described by Equation 2. My first reaction was that I did not like the sum of absolute values in the objective, so I reformulated the problem into

\begin{align} \min_{\beta, t} \sum_{i=1}^n (y_i - x_i^\top \beta)^2 + \lambda (t_1 + … + t_p) \cr \beta_i \leq t_i, i=1,…, p \cr -t_i \leq \beta_i, i=1,…, p. \end{align}

Then, I wrote the corresponding saddle point problem (this is Lagrangian Duality)

\begin{align} \max_{\theta \geq 0, w \geq 0} \min_{\beta, t} \sum_{i=1}^n (y_i - x_i^\top \beta)^2 + \lambda (t_1 + … + t_p) + \sum_{i=1}^p\theta_i (\beta_i - t_i) + w_i (-t_i - \beta_i). \end{align}

Notice we were able to get rid of the absolute value! From here I wrote KKT conditions, but essentially ended up with something like: “If I knew the sign of every non-zero coefficient, then I could find a closed form solution for $\beta$.” But I dont think there is a way to know the signs of the coefficents before you’ve solved the problem. So, to continue the argument I would have to guess (and) solve an exponential number of linear systems. This was obviously going in the wrong direction, so I decided to stop. In hindsight, I shouldn’t have been afraid of dealing with the non-differentiability of the absolute value, with just the knowledge of subgradients I (maybe) could have arrived at a solution myself.